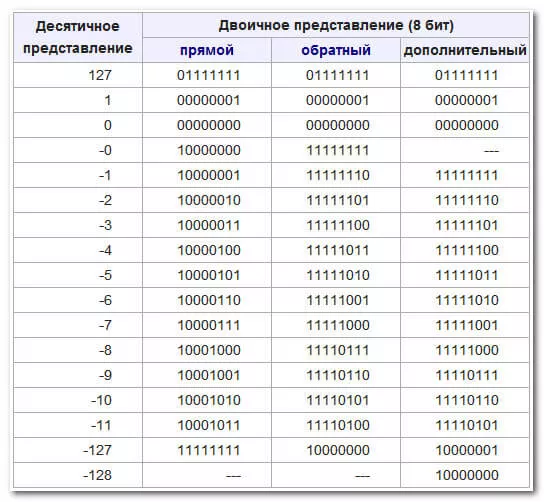
В двоичной системе представление отрицательных чисел не так интуитивно понятно, как представления положительных. В основе работы с отрицательными числами в двоичном формате лежат специальные способы кодирования, которые позволяют выполнять математические операции над числами разных знаков. Среди них особо выделяются дополнительные коды, обратные и прямые коды, основанные на использовании знаковых разрядов. В этой статье мы рассмотрим, как эти системы представления работают и как они применяются при переводе отрицательных чисел из десятичной системы в двоичную.
Понимание двоичной системы
Двоичная система — это основа современной цифровой электроники и компьютерных технологий. Каждый разряд в двоичном числе может принимать значение равное 0 или значение равное единице, что делает ее идеальной для представления логических состояний и электрических цепей. В контексте вычислений, двоичные представления чисел существенно упрощают арифметические операции, в особенности модулю 2, что особенно важно в применении в информационных технологиях.
История двоичной системы
Двоичная система счисления была известна еще в древние времена, но свое бурное развитие она получила только в XX веке с появлением компьютерных технологий. В 1937 году американский математик Джордж Стибиц использовал двоичные числа для создания одного из первых цифровых компьютеров, что открыло эру информационных технологий и по сей день двоичная система остается их неотъемлемой частью.
Отрицательные числа и их представление
В десятичной системе отрицательные числа обозначаются просто: перед числом ставится знак минус. Но в двоичной системе счисления нет символов, кроме ‘0’ и ‘1’, и поэтому для выражения отрицательности числа используются дополнительные способы. Самым распространенным является использование знакового бита, который располагается в старшем разряде двоичного числа. Если знаковый бит установлен в ‘1’, это обычно указывает на отрицательное число, если в ‘0’ – на положительное или ноль.
Отличие отрицательных чисел от положительных
Одним из ключевых отличий двоичного кодирования отрицательных чисел от представления положительных является то, что в зависимости от используемого метода, могут применяться дополнительные математические преобразования. Например, при использовании дополнительных кодов, значение отрицательного числа формируется путем переворота всех битов положительного числа и добавления к результату единицы.
Практическое применение отрицательных чисел
Отрицательные числа играют важную роль во многих областях, включая компьютерное программирование, цифровую обработку сигналов и финансовые расчеты. Понимание того, как они представлены в двоичном коде, необходимо разработчикам программного обеспечения, инженерам и аналитикам данных, чтобы правильно интерпретировать данные и управлять электронными устройствами.
Способы представления отрицательных чисел в двоичной системе
- Прямой код — В прямом коде знаковый бит указывает на знак числа, а остальные биты представляют абсолютное значение числа. Прямые коды используются для упрощения понимания числовых последовательностей, но не всегда эффективны при выполнении арифметических операций.
- Обратный код — обратные коды задаются инвертированием всех битов положительного числа в случае, если исходное число отрицательное. При сложении обратных кодов особенно важно следить за переполнением разрядной сетки.
- Дополнительный код — Самым распространенным методом является дополнительный. Он формируется инверсией всех битов прямого кода и добавлением к полученному значению единицы. Этот способ удобен для проведения арифметических операций, так как позволяет использовать одну и ту же логику сложения как для положительных, так и для отрицательных чисел.
| Метод | Описание | Пример для числа ‘-5’ |
|---|---|---|
| Прямой код | старший бит – знаковый бит, остальные биты представляют модуль числа | 1101 |
| Обратный код | все биты абсолютного значения числа инвертируются | 1010 |
| Дополнительный код | обратный код увеличивается на единицу | 1011 |
Процесс преобразования отрицательных чисел в двоичный код
- Пошаговая инструкция — Для того чтобы получить дополнительный код отрицательного числа, сначала запишите число в двоичной форме как если бы оно было положительным. Затем инвертируйте все биты, и, наконец, прибавьте к инвертированному значению единицу. Этот процесс обеспечивает корректное сложение положительных и отрицательных чисел в двоичной арифметике.
- Примеры преобразования — Рассмотрим примеры преобразования числа -5 в различные двоичные коды. В прямом коде это будет 1101, в обратном 1010, и в дополнительном 1011. Эти представления показывают, как может изменяться двоичный код одного и того же отрицательного числа в зависимости от выбранного метода кодирования.
Практические советы и рекомендации
- Частые ошибки и как их избежать — Самая распространенная ошибка — это неправильный перевод числа из десятичной системы в двоичную. Для предотвращения ошибок всегда проверяйте правильность перевода десятичного числа в двоичную систему, особенно внимательно относясь к знаковым битам. Проверка логической правильности арифметических операций также поможет избежать путаницы.
- Использование программных инструментов — Для упрощения процесса преобразования и минимизации ошибок рекомендуется использовать программные инструменты. Специализированные калькуляторы и разработанные алгоритмы могут автоматически выполнять перевод чисел и операции над ними, упрощая работу с двоичными данными.
Итоги
В статье рассмотрены основные способы представления отрицательных чисел в двоичной системе, которые являются ключевыми для понимания и работы с компьютерными системами. Знание и понимание прямых, обратных и дополнительных кодов, а также навыки их применения обеспечивают точность и эффективность вычислительных процессов. Практическое применение этих методов повышает вероятность корректной работы программного обеспечения и обработки информации в цифровых устройствах и системах.
Часто задаваемые вопросы
-
Вопрос 1: Почему для представления отрицательных чисел в компьютерах не используют обозначение, аналогичное десятичной системе, с минусом?
Ответ: В двоичной системе используются только два символа — 0 и 1. Введение знака минус потребовало бы использования третьего символа, что сделало бы систему более сложной для электронных вычислений. Использование знакового бита — это более эффективный способ представления отрицательности числа в двоичном коде.
-
Вопрос 2: Можно ли использовать прямой код для арифметических операций с отрицательными числами?
Ответ: Хотя прямой код удобен для понимания и интерпретации, он не всегда эффективен для выполнения арифметических операций, особенно когда речь заходит о сложении и вычитании чисел с разными знаками. Для этих операций чаще используется дополнительный код.
-
Вопрос 3: Чем дополнительный код отличается от обратного кода?
Ответ: Обратный код получается инвертированием всех битов положительного числа, в то время как для получения дополнительного кода к результату инверсии еще прибавляется единица. Это делает дополнительный код более удобным для арифметических операций в двоичной системе.
-
Вопрос 4: Каковы преимущества и недостатки использования дополнительного кода?
Ответ: Преимуществами дополнительного кода являются универсальность для представления положительных и отрицательных чисел, а также упрощение арифметических операций, таких как сложение и вычитание. Недостатком же может быть необходимость дополнительных шагов при переводе числа в этот формат.
-
Вопрос 5: Существуют ли другие способы представления отрицательных чисел в двоичной системе, кроме рассмотренных?
Ответ: Кроме прямого, обратного и дополнительного кодов, существуют и другие, менее использованные методы представления, такие как коды со сдвигом и BCD-коды (двоично-десятичные). Однако на практике они встречаются реже и имеют более узкую специализацию.